El mundo es un pañuelo: la teoría de los 6 grados de separación 🤯

En estos momentos en los que estamos viviendo una pandemia mundial que se expande de forma exponencial, podemos visibilizar cómo de unida está la sociedad de nuestro planeta. Estoy hablando, por tanto, de la teoría de los 6 grados de separación, también conocida como la teoría del mundo pequeño. Una de tantas teorías o paradojas matemáticas que podría situarse en contra de nuestra propia intuición.

6 grados de separación

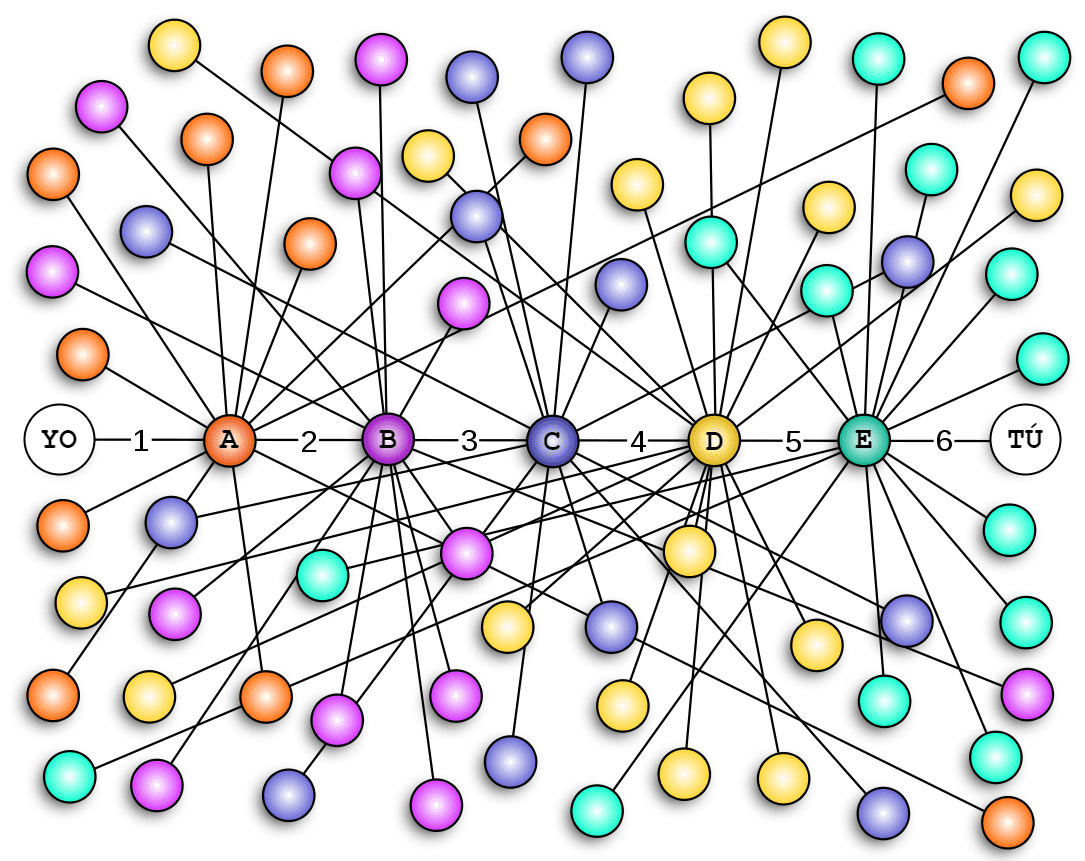
La teoría de los 6 grados de separación fue inicialmente propuesta en 1930 por el escritor húngaro Frigyes Karinthy en un relato de ficción llamado «Chains» y fue recogida a su vez en 1990 en la obra de teatro «Six Degrees of Separation» de John Guare y en 2003 en el libro «Six Degrees: The Science of a Connected Age», del sociólogo Duncan Watts. Esta teoría establece que cada persona del mundo puede llegar a conectarse con cualquier otra dando tan sólo 6 saltos entre personas, es decir, a través de 5 intermediarios. Yo conozco a A, A conoce a B, B conoce a C, C conoce a D, D conoce a E y E te conoce a ti. Ya estamos conectados por A, B, C, D y E. 5 intermediarios y 6 enlaces que nos unen a través de ellos. Y os preguntaréis: ¿por qué 6 saltos?

Debemos empezar suponiendo un número de personas conocidas por cada ser humano del planeta en media. Cuantas más personas conozca cada ser humano directamente, es decir, que estén unidas por 0 intermediarios, un solo salto, menos saltos serán necesarios para alcanzar a cualquier otro ser humano del planeta.

La teoría de los 6 grados de separación parte de que cada persona conoce de media, entre amigos, familiares o compañeros de trabajo, a unas 100 personas. De esta manera, si cada uno nos relacionamos con 100 personas diferentes, y cada una de esas 100 personas con otras 100 personas diferentes de las anteriores, en tan sólo 2 saltos llegaríamos a 10 mil personas. Esto es el resultado de un crecimiento exponencial, elevando el número de personas conocidas por cada individuo, en este caso 100, al número de saltos que lo conecten con otro individuo. Partiendo de esto, en un tercer salto conoceríamos a 1 millón de personas, en un cuarto salto a 100 millones, en un quinto salto a 10 mil millones y en un sexto y último salto estaríamos conectados con 1 billón de personas.

Esta cifra es sin duda mucho mayor que la población mundial, que se encuentra en torno a un valor de 7.53 miles de millones de personas. Podríamos decir incluso que en el quinto salto ya habríamos logrado conectar a toda la población. Digamos que con 6 saltos ya está más que asegurado. De hecho, es necesario darse cuenta de que, para llegar a conectar verdaderamente a 1 billón de personas, cada una de las 100 personas que conozco yo deben ser distintas de las 100 personas que conoce la persona A y a su vez distintas de las que conoce la persona B, y así sucesivamente hasta los conocidos por la persona E, que es quien dará el sexto y último salto de conexión. Si alguna de esas personas coincidiera con alguna ya contemplada en los saltos anteriores, estaríamos volviendo hacia atrás y repitiendo enlaces de conexión. Es por esto que la teoría no se queda con el número de saltos que cubre con mayor exactitud a 7.53 miles de millones de personas y trata de abordar una solución menos optimista, determinando un valor de 6 saltos definitivos.

De hecho, en la práctica, las 100 personas que conoce A, la persona del segundo nivel, seguramente no serán todas distintas de las que yo conocía en el primer nivel, tendremos amigos comunes, y lo mismo ocurrirá entre el resto de niveles. Por tanto, el número de contactos de segundo nivel no sería 10 mil, sino un valor sustancialmente menor, lo cual repercutiría en el millón de personas conectadas en un tercer nivel, que también sería menor, y así hasta el último nivel, en el cual tampoco conseguiríamos llegar a conectar 1 billón de personas con seguridad, pero sí 7.53 mil millones.

Explicación matemática

Si nos ceñimos a las matemáticas, con una simple fórmula podemos ser capaces de, dado un número de saltos S con los que conectar a la población mundial, determinar cuántas personas distintas P es necesario que conozca cada individuo de la cadena. Viendo el problema desde el otro lado, podemos determinar también, asumiendo un número determinado de personas P que cada individuo conoce distintas del resto, cuál será el número de saltos o enlaces S que nos conecte a todos.

Para la primera opción, asumiendo un número de saltos igual a 6 y sabiendo que somos 7.53 miles de millones de personas en el mundo, se calcula que cada persona debe conocer a 44.27 personas distintas en un primer nivel, no comunes a los conocidos de segundo o mayor nivel. Como no se conocen personas por partes, digamos que debemos conocer como mínimo a 45 personas distintas de los conocidos del resto para que esta teoría se cumpla con seguridad.

Trabajando con la segunda opción y asumiendo por tanto 45 personas conocidas y distintas a las conocidas por el resto de personas de los distintos niveles de conexión, se calcula el resultado inverso: se necesitan 6 saltos para conectarnos a todos.

Este resultado matemático corresponde a la teoría de los 6 grados de separación, que parte de 100 personas conocidas por cada individuo y, asumiendo que no todas van a ser distintas o nuevas en cada nivel, obtiene el número de saltos para el cual pequemos de exceso pero no de defecto. Esto es lo mismo que asumir que con total seguridad 45 personas serán distintas en todos los niveles y con ello, matemáticamente, llegamos a 7.53 millones de personas en un total de 6 saltos.

En caso de pensar que no van a ser 45 las personas que conozcamos distintas de las que conozcan los demás, si no que serán menos, podremos resolver el cálculo numérico y simplemente obtendremos un número de saltos mayor.

Demostración basada en datos

En 2011, Facebook realizó un estudio denominado «Anatomy of Facebook»[1] con todos los usuarios activos en su red social en ese momento, los cuales representaban un 10 % de la población mundial, y se analizaron sus conexiones en base a los amigos de cada usuario. Con este estudio se descubrió que a través de 5 grados de separación se podía conectar al 99.6 % de pares de usuarios conectados en la red. La distancia media entre usuarios tomaba un valor de 4.7. Por el décimo aniversario de esta red social, en 2016, se procedió a evaluar de nuevo estos datos, con más usuarios en Facebook y, a su vez, más interconectados. En este nuevo estudio se vio acortada la distancia entre dos personas en el mundo, que alcanzó un valor medio de 3.57 grados de separación.

El mismo experimento se realizó también con la red social Twitter en 2011[2] y se observó un valor medio de niveles de separación entre usuarios incluso menor que en Facebook: 3.43 grados frente a los 4.7 obtenidos en Facebook en el mismo año.

Otro experimento curioso basado en las ingentes cantidades de datos que se manejan actualmente gracias a Internet y las redes sociales, es conocido como «Oracle of Bacon»[3]. Este experimento, que se centró en evaluar esta teoría en un grupo determinado de la población, se basó en calcular el número de niveles de unión entre cualquier persona dentro del terreno cinematográfico y Kevin Bacon. Se considera conocidos a aquellos actores o actrices que hayan participado alguna vez en la misma película. Si este número resulta menor o igual a 3 para dos personas escogidas al azar, significará que esas dos personas están a un número de saltos menor o igual a 6, usando de intermediario a Kevin Bacon.

Otros problemas exponenciales: epidemias

Al igual que ocurre en esta teoría de conexión entre personas en la que los conocidos de un individuo crecen exponencialmente con cada nuevo enlace, en una epidemia el número de infectados por un virus también lo hace. De esta manera, sólo un pequeño número de enlaces son necesarios para que el conjunto de conocidos se convierta en la población humana mundial, o para infectar con un virus a todo un país, continente, o planeta.

La Organización Mundial de la Salud (OMS) estimó que la tasa de contagio (R0) del coronavirus estaba entre 1.4 y 2.5, aunque otras estimaciones hablaron de un rango entre 2 y 3. Esto quiere decir que cada persona infectada por coronavirus puede a su vez infectar a entre 2 y 3 personas. Tomando así una tasa de contagio R0 de valor 2.5, podríamos estimar el número de saltos S que debería realizar el virus para contagiar a toda la población mundial. Este valor resulta tan sólo 25 saltos.

La rapidez con la que el virus vaya a dar esos saltos e incluso la probabilidad de que llegue a darlos en su totalidad, depende de varios factores como la duración del periodo infeccioso del virus en nuestro organismo, o el número de personas susceptibles de contagio con las que pacientes afectados entran en contacto. Por tanto, frenar una epidemia depende en gran parte de nosotros mismos. De la inmunidad de grupo cuando existe vacuna, y cuando no: de nuestros viajes, de nuestros contactos, de nuestros movimientos. Quédate en casa.

“Parece magia, pero son matemáticas”

Clara Grima